!! NOW AVAILABLE ON THE APPLE APP STORE !!

Collatz Conjecture and Computational Mathematics

An Algorithmic Approach

Admitting my rather recent introduction and study of the Collatz Conjecture I have been perplexed by the problem definition that is different from the one that I presented in my last posting titled “Collatz and The Three Bears”. I have heard various mathematicians present a conceptional problem definition that does not complete but rather, in the 3n + 1 problem, closes upon the 4 -> 2 -> 1 -> 4 … infinite loop. This is an heresy from the computational perspective since it is difficult to solve a generalized problem that by definition does not end with a final, or accepting state. Given that the formal definition of a finite state automata (FSA) or Turing machine is defined to be:

That is to say that there needs to be a set F which is a subset of the finite, non-empty set of states Q that defines a final or accepting state. Thus, in my previous posting step two of the 3n + 1 algorithm is to halt if the computed value is equal to one.

There are two very different approaches to mathematics. In 1973, a mathematical conference was held jointly by the American Mathematical Society and the Mathematical Association of America, and titled the “Conference on the Influence of Computing on Mathematical Research and Education”. It was here that Peter Henrici of Swiss Federal Institute of Technology Zürich (Eidgenössische Technische Hochschule or ETH) coined the terms “algorithmic mathematics” and “dialectic mathematics”. And this distinction as quoted directly from Peter Henrici’s paper was:

“Dialectic mathematics is a rigorously logical science, where statements are either true or false, and where objects with specified properties either do or do not exist. Algorithmic mathematics is a tool for solving problems. Here we are concerned not only with the existence of a mathematical object, but also with the credentials of its existence. Dialectic mathematics is an intellectual game played according to rules about which there is a high degree of consensus. The rules of the game of algorithmic mathematics may vary according to the urgency of the problem on hand.”

And further in the paper

“Dialectic mathematics invites contemplation. Algorithmic mathematics invites action. Dialectic mathematics generates insight. Algorithmic mathematics generates results.”

We are most familiar with mathematics of the dialectic sort. But surprisingly, algorithmic mathematics does not require a computer. In fact, one of the earliest examples of algorithmic mathematics is from a Babylonian clay tablet from the 18th century BC that defines an algorithm for approximating the square root of 2. The steps are simple:

• Step 1: Try and guess the square root of 2.
• Step 2: Divide your original number by your guess.
• Step 3: Find the average of your guess and the result of step 2.
• Step 4: if the difference of the guessed number and the average is close enough then stop, otherwise go to step 2 using the average as your next guess.

To this day we have no function f(n) = Pn where Pn is the nth prime. The sequence of prime numbers are found through one of many sieve algorithms from Eratosthenes through Atkins or a wheel sieve, which themselves are examples of algorithmic mathematics. Do we then propose that an Algorithmic approach will not be able to produce a proof of the conjecture since it is by nature outside of the dialectic world of true/false? Remember Bertrand Russell and Alfred Whitehead’s Principia Mathematica? Or can an algorithmic approach lead to insights that will allow for a Dialectic proof? What if we do not attempt to provide a dialectic proposition of truth or falsehood, but rather focus on a computational model that will allow us to perceive insight leading to understanding how something works.

I approach this problem algorithmically using a computation model of the Natural Numbers, and consequently would like to introduce the product of my efforts and the first offering from Sophwares – The Collatz Calculator. I am curious as to the interest in such an application. At present, I have a version for IOS targeted to an iPhone or iPad, and a version for MacOS for the Apple Mac computer that soon, I hope, will be available from the Apple App Store.

Interested?

Here are some screen shots.

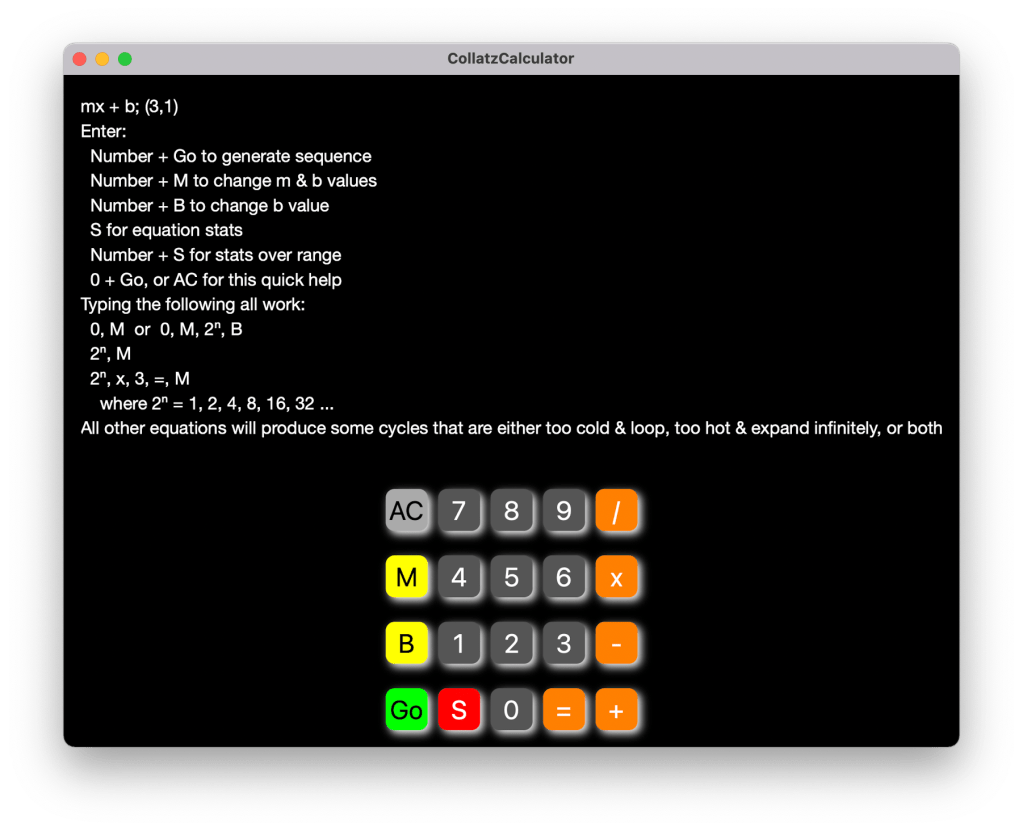
When you start the application
you will see the quick help screen:

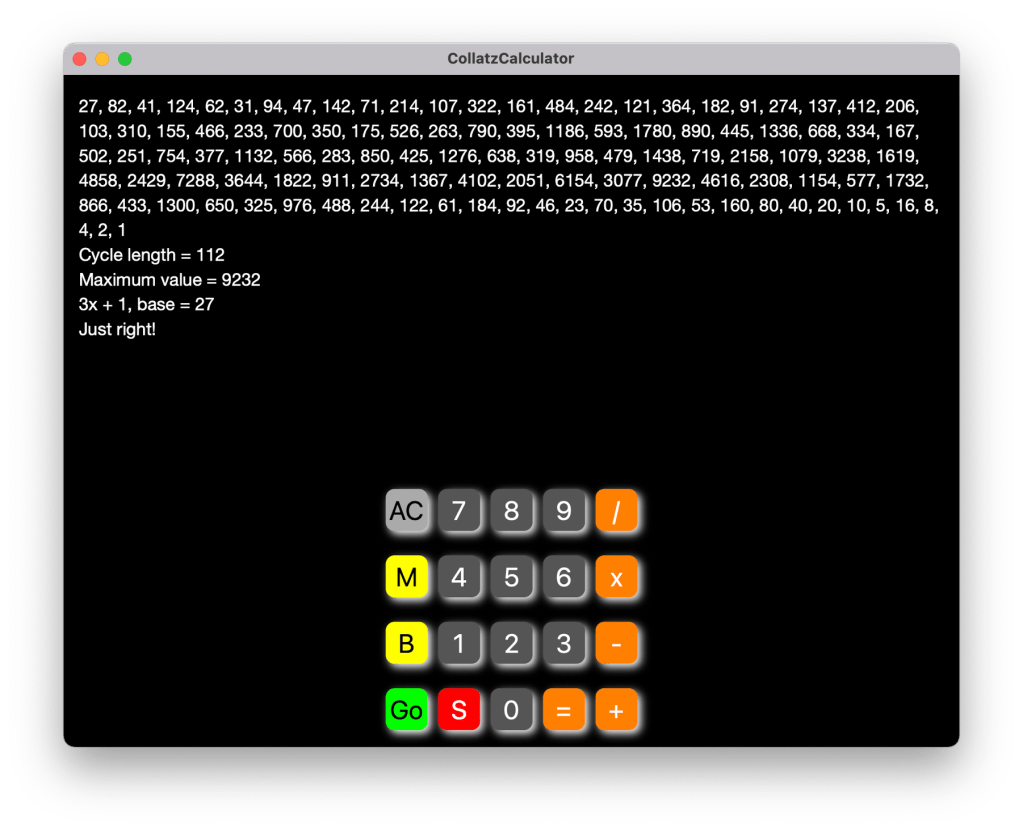
When you type 27 and Go you
will see the sequence generated
for 27:

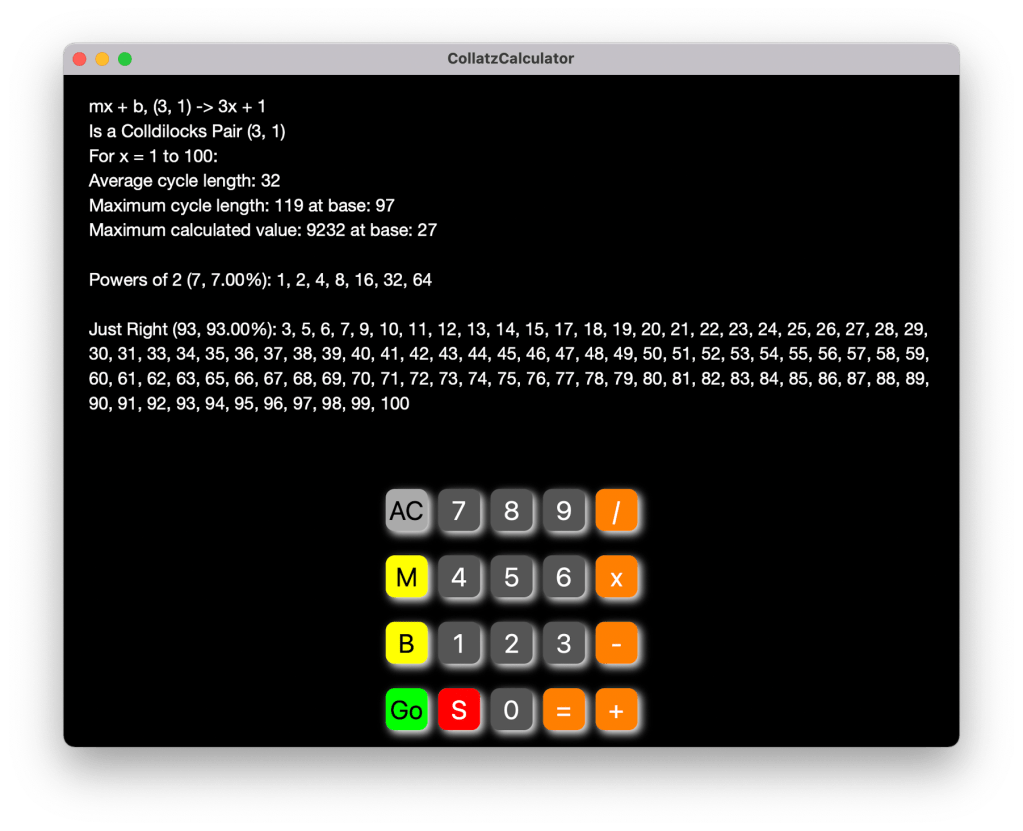
When you type S, you will see
the stats for n = 1 to 100:

Since the conjecture suggests that the sequence generated for any value of n will resolve to one for 3x + 1, it becomes more interesting when you change the formula. This is accomplished with the M and B buttons. The M button will allow you to set the M value and calculates a value for b based on whether M is the first value of a Colldilocks pair (M, B). If M = 0, B will be set to 2. If M is a power of 2, then B will be set to the same power of 2, and if M = 3 times a power of 2, B will be set to the power of 2. Otherwise, M will be set to any value that is not the first value of a Colldilocks set pair and B will be set to 1. B will be set to whatever value you type as a number, and press the B button.

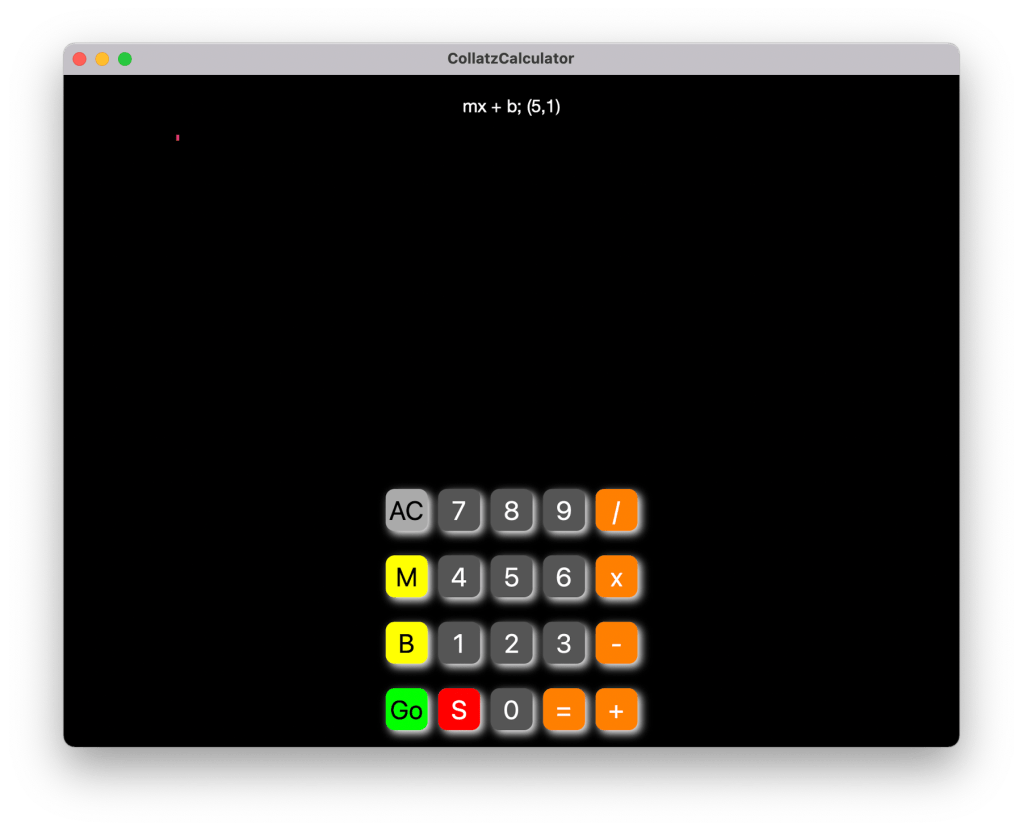
When you type 5, M you will
see the (M,B) pair set to (5, 1):

When you type S, you will see
the stats for n = 1 to 100 for
5x + 1:

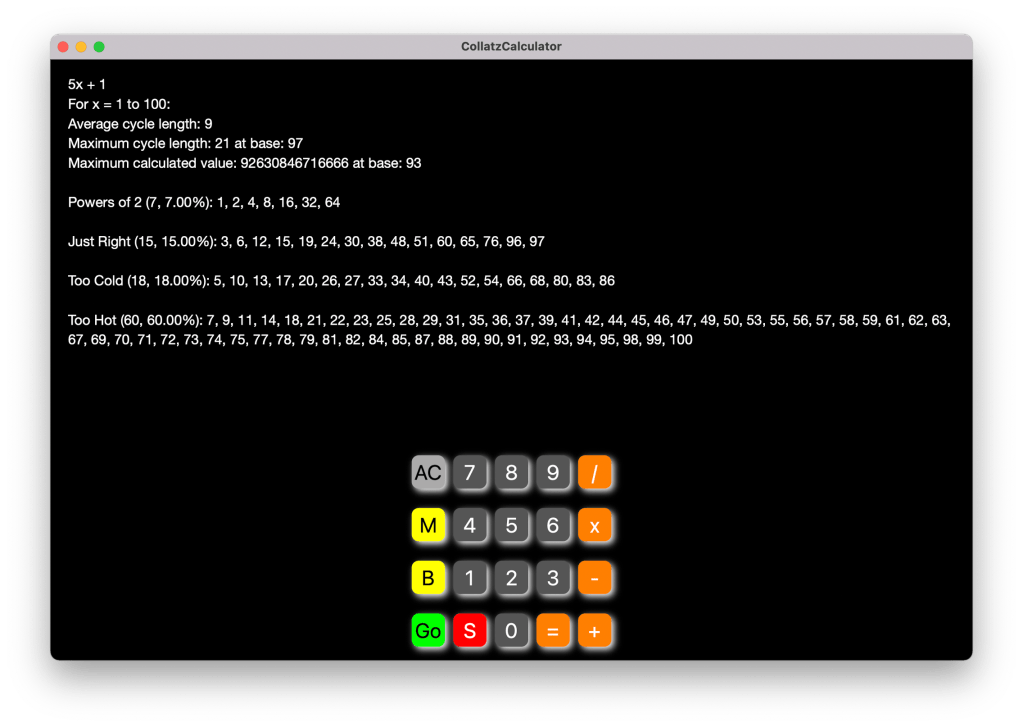
The stats page indicates the formula under consideration. It will show the range of x, which can be set by first typing the maximum value for x (default 100). But be careful here, especially on a iPad or iPhone. The larger the range, the busier your calculation since it has to generate all sequences for all x between 1 and N. It also reports the average cycle length (excluding the infinite too hot, and too cold cycles). It will report the maximum cycle length over the range and the first value for x that generates a cycle of that length. It will also show the highest calculated value over the range and the first value for x that reaches that peak. In cases where the x value is too cold and loops, it will show you at which step the number repeats and the index of the first occurrence of the repeating value. And if the value of x is too hot, it will predict when it believes that the values will simply continue an upward trend towards infinity. It will also present lists of x values that are powers of 2, and if applicable, the list of x values that will resolve to 1 (just right), the list of x values that will produce a loop (too cold), and the list of x values that it predicts will lead to infinite expansion (too hot). If you type one of the values of x displayed on the stats page it will display the cycle for that value.

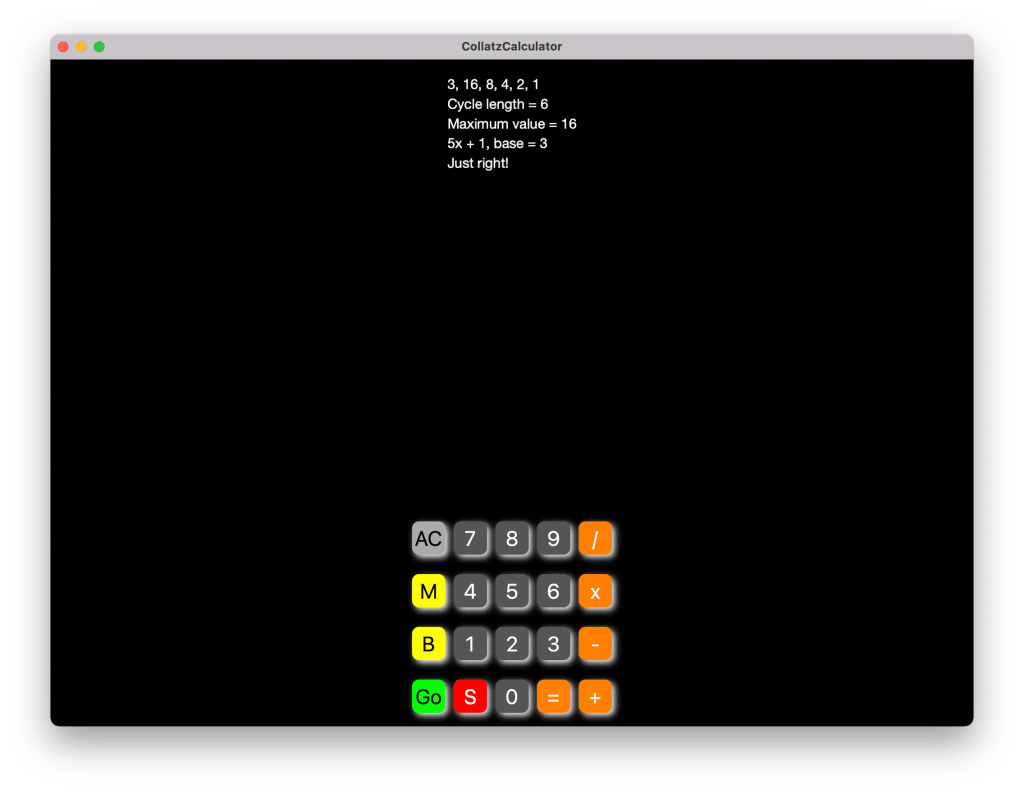
Now when you type 3 and Go
you will see the “just right”
sequence generated for x = 3
when y = 5x +1:

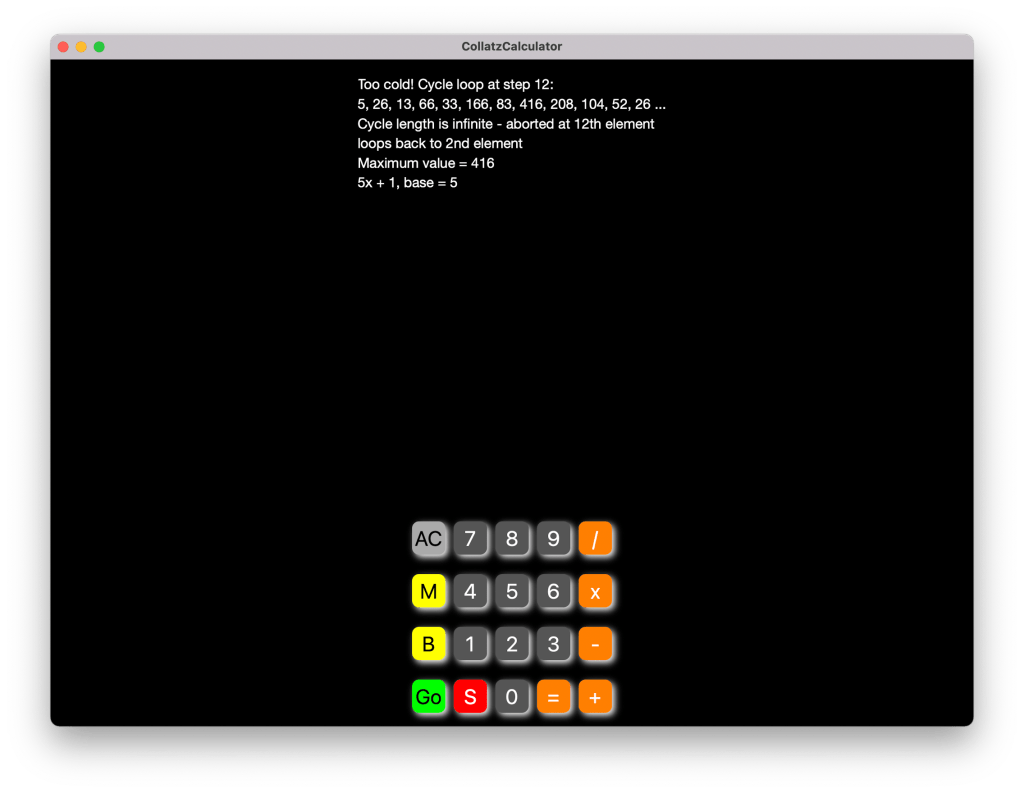
If you type 5 and Go you will
see the “too cold” sequence
generated for x = 5
when y = 5x +1:

And if you type 99 and Go
you will see the “too hot”
sequence generated for x = 99
when y = 5x +1:

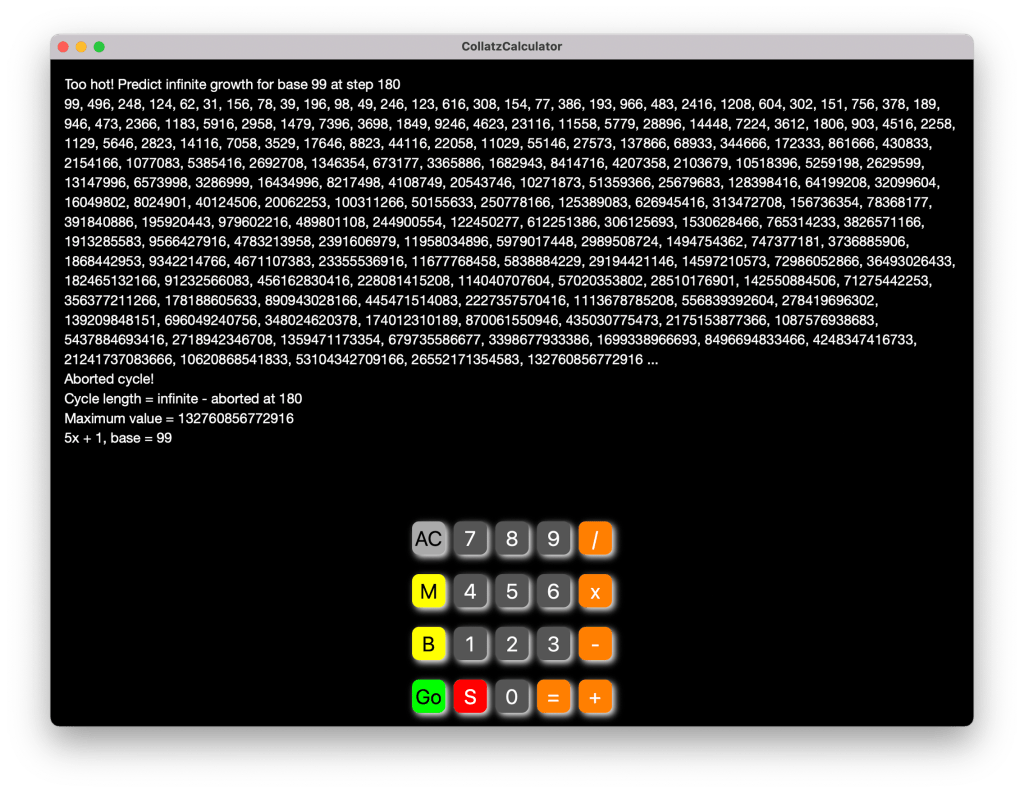
The Collatz Calculator will allow you to study the Collatz Conjecture across any value of the generalized linear equation y = mx + b for all values of m, x, and b.